算法题解4_最长公共子序列
如果字符串一的所有字符按其在字符串中的顺序出现在另外一个字符串二中, 则字符串一称之为字符串二的子串。
解法
经典的用动态规划算法解决。
使用一个矩阵记录信息.
状态转移方程如下:
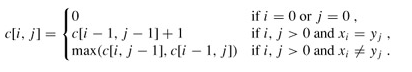
Java代码如下:
public int lcs(String str1, String str2) {
if ( null == str1 || 0 == str1.length() || null == str2 || 0 == str2.length() )
return 0;
int[][] table = new int[ str1.length() + 1 ][str2.length() + 1];
for (int i = 0; i <= str1.length(); i++) {
for (int j = 0; j <= str2.length(); j++) {
if ( 0 == i || 0 == j )
table[i][j] = 0;
else if (str1.charAt(i - 1) == str2.charAt(j - 1))
table[i][j] = table[i - 1][j - 1] + 1;
else
table[i][j] = Math.max(table[i - 1][j], table[i][j - 1]);
}
}
// 求出具体的最长公共子序列
int index1 = str1.length();
int index2 = str2.length();
StringBuilder sb = new StringBuilder();
while ( index1 > 0 && index2 > 0 ) {
if ( str1.charAt(index1 - 1) == str2.charAt(index2 - 1) ) {
index1--;
index2--;
sb.append( str1.charAt(index1) );
}
else if ( table[index1][index2] == table[index1 - 1][index2] )
index1--;
else
index2--;
}
System.out.println( sb.reverse().toString() );
return table[ str1.length() ][str2.length()];
}
Written on January 23, 2016
